To approve our theory of designing a recombinant chitinase showing antifungal activity better compared to wild-type chitinases, several models have been developed and optimized. We have tried to model all the essential aspects that cover our project.
These models give us an overview of the activity of the enzymes that could be verified through experiments. Nonetheless, they are a reliable source of information.
Fungal growth models
The team has identified 7 fungal species through morphology and Sanger sequencing. To check the activity of our chitinase enzymes, we need to determine the growth rate and lag phase of the species to compare it with the changed parameters when inflicted with the extracted protein.
To analyze the growth of fungus two different models were used:
Surface area based model
Fungus when grown on a Petri plate in a PDA (Potato dextrose agar) medium, tends to grow radially (given no contamination). The increasing radius and hence the increasing surface area is a parameter that can be used to check its rate of growth over time.
The unidentified samples were inoculated in Petri plates and observed for 4-5 days to capture images of the growing fungus.
Note: It was assumed that inoculum for all fungal species was of equal size.
The images were aligned and analyzed using the ImageJ software, where the radius and the corresponding area were measured.
The team has considered several growth models, which were mostly used for bacterial growth, yet can be used for fungal growth as well.[4]
Gompertz
\begin{equation} y=y_{0}+C(e^{-e^\frac{\mu e(\lambda-t)}{C+1}}) \end{equation}
Logistic
\begin{equation} y=y_{0}+\frac{C}{1+ e^(\frac{4\mu(\lambda-t)}{C+2})} \end{equation}
Richards
\begin{equation} y=y_{0}+\frac{C}{(1+\beta e^{1+\beta}e^{((\frac{\mu}{e})(1+\beta)(1+\frac{1}{\beta})(\lambda-t))})^{\frac{1}{\beta}}} \end{equation}
Where, y0= Initial log count or absorbancey= Log count or absorbance at time t
mu= Maximum growth rate
lambda= Lag time
C= Increase in log count or absorbance from y_0 to y_max
beta= Model coefficient.
These 3 equations were used to fit the curve and finding the unknown parameters. It has been calculated that the Gompertz model of growth gives us the least RMSE, hence proving to be the best model for our data.
Few drawbacks of this method:
- The growth of the fungus is confirmed to the surface area Petri plate itself, once the fungus covers the plate, it starts growing volumetrically, making it difficult to analyze the growth.
- Most of the fungus present on our campus are sporulating. The spread of spores within the plate causes several colonies to grow together, rendering the experiment useless, as different colonies superimpose on each other and no proper radius is visible.
- Sometimes, the fungal species may not grow radially, but in a non-uniform shape, increasing the manual labor of calculating the area.
O.D. based growth model
Scattering of light by a replicating population over time, and hence the changing OD is a good proxy for the growth of fungus instead of measuring its changing radius.[1] The fungal species were grown in a 96-well plate in a PDB (Potato dextrose broth) medium, with spores suspended in PBS (Phosphate buffered saline), and observations were taken 4-5 days for an interval of 6 hours at 605nm.
Note: The assumption is made that the spore suspension has been uniformly distributed throughout the well.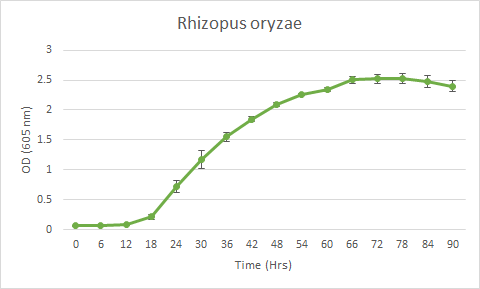
Figure 1. bla bla bla...
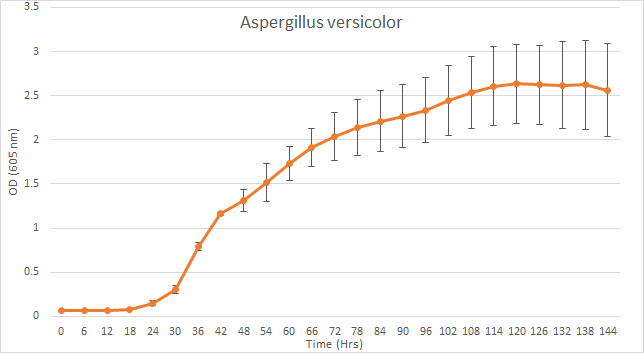
Figure 2. bla bla bla...
Limitations of this method:
- The fungus sometimes starts growing along the walls, hampering the OD.
- The plate was kept in an incubator-cum-shaker at 28 degrees celsius, but the heat inside the incubator causes the media in the plate to evaporate and dry up. Hence, a humidity chamber needs to be made to minimize the evaporation of media from the plate.
IC50 of an antifungal-Nipagin
Nipagin, being a methylparaben, is an antifungal agent, which is primarily used in cosmetics, food preservatives.[2] We carried out an antifungal assay using Nipagin, to calculate its IC50 for the fungal species identified by the team. This very same experiment would be repeated with the purified protein of our interest to calculate its IC50 for different fungal species. We wish to check the applicability of the models which calculate IC50 using Nipagin, which then would be used of our protein.
IC50 of the antifungal here would indicate how much of the chemical would be needed t inhibit, in vitro, the given fungal species[3]. Lower the IC50, better the efficiency of the antifungal.
An initial trial in doing the experiment, with antifungal concentration starting from 1000μg/mL, with serial dilutions of ½ till the final concentration of 0.488μg/mL gave us the IC50 as follows:
- Rhizopus oryzae: 230.46μg/mL
- Aspergillus versicolor: 288.916μg/mL
The experiment was repeated again to verify the results with different mathematical methods. Since the IC50 of Nipagin for both the fungus came about 200-300μg/mL range, the concentrations were started from 800μg/mL till 0.5μg/mL, with a change of concentration by subtraction of 100μg/mL.
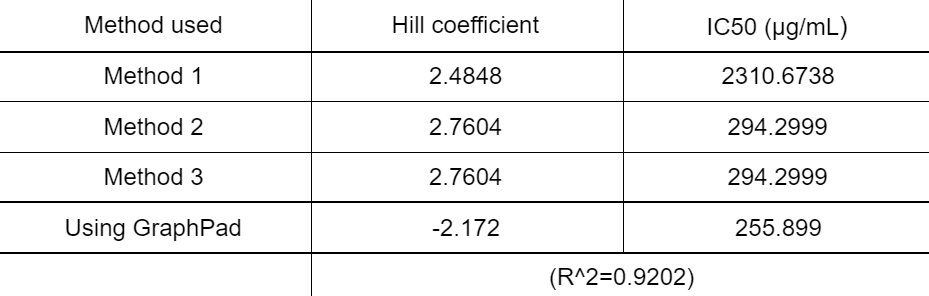
The inhibition percentage has been calculated using 3 different methods:
- Method 1
- Method 2
- Method 3
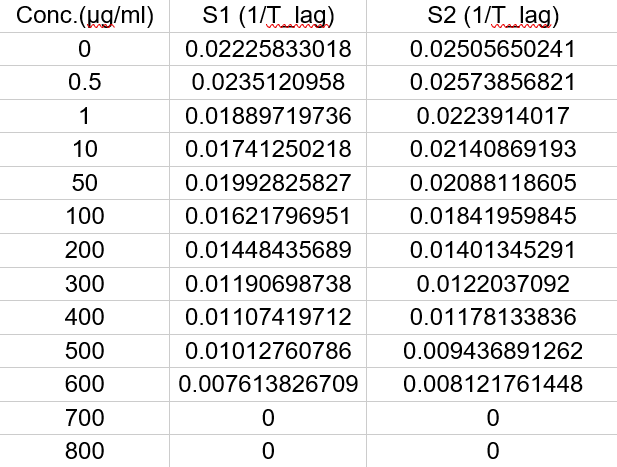
Data for Aspergillus versicolor
Where,
S1 = Sample 1
S2 = Sample 2
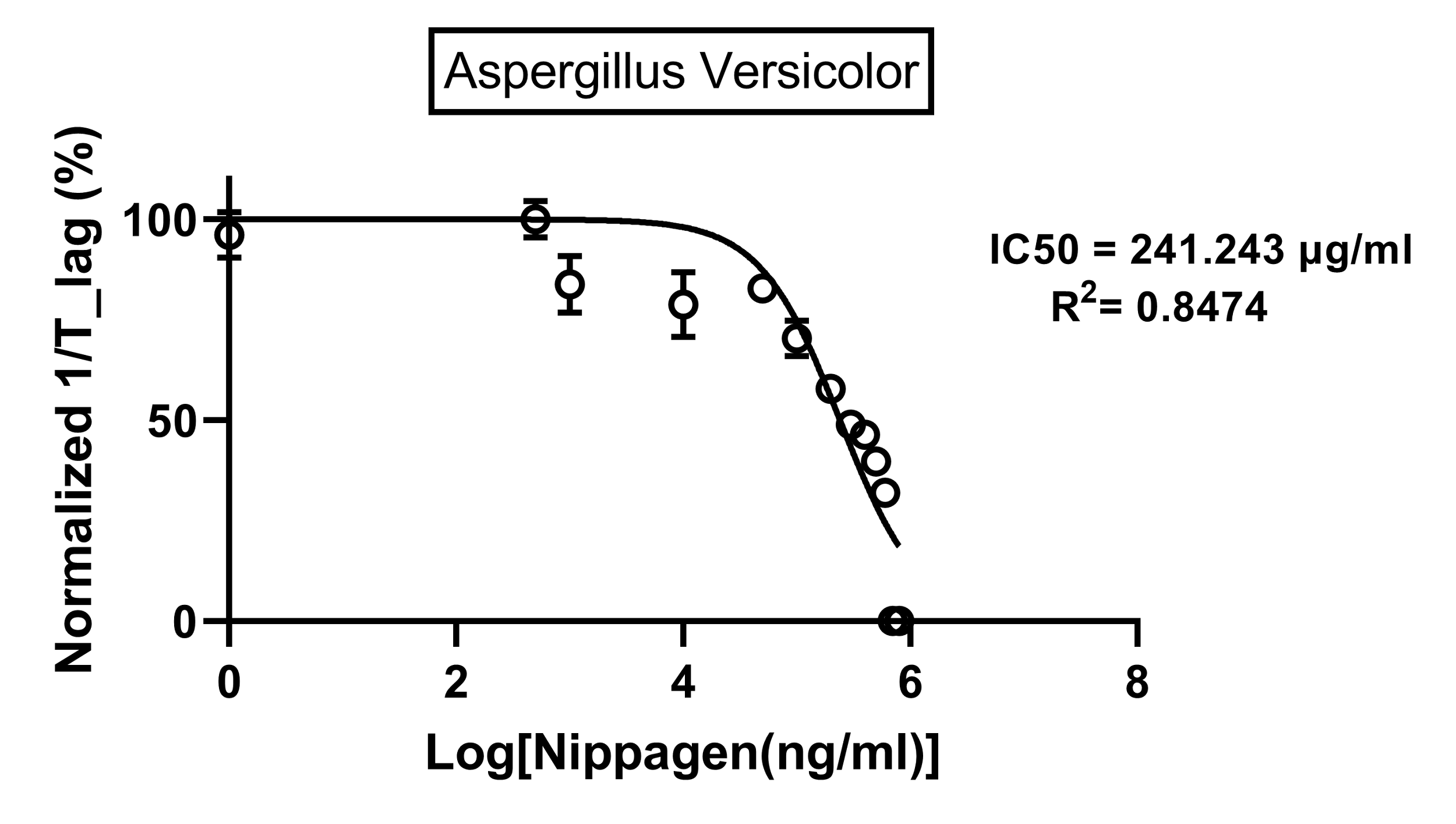
Figure 4.
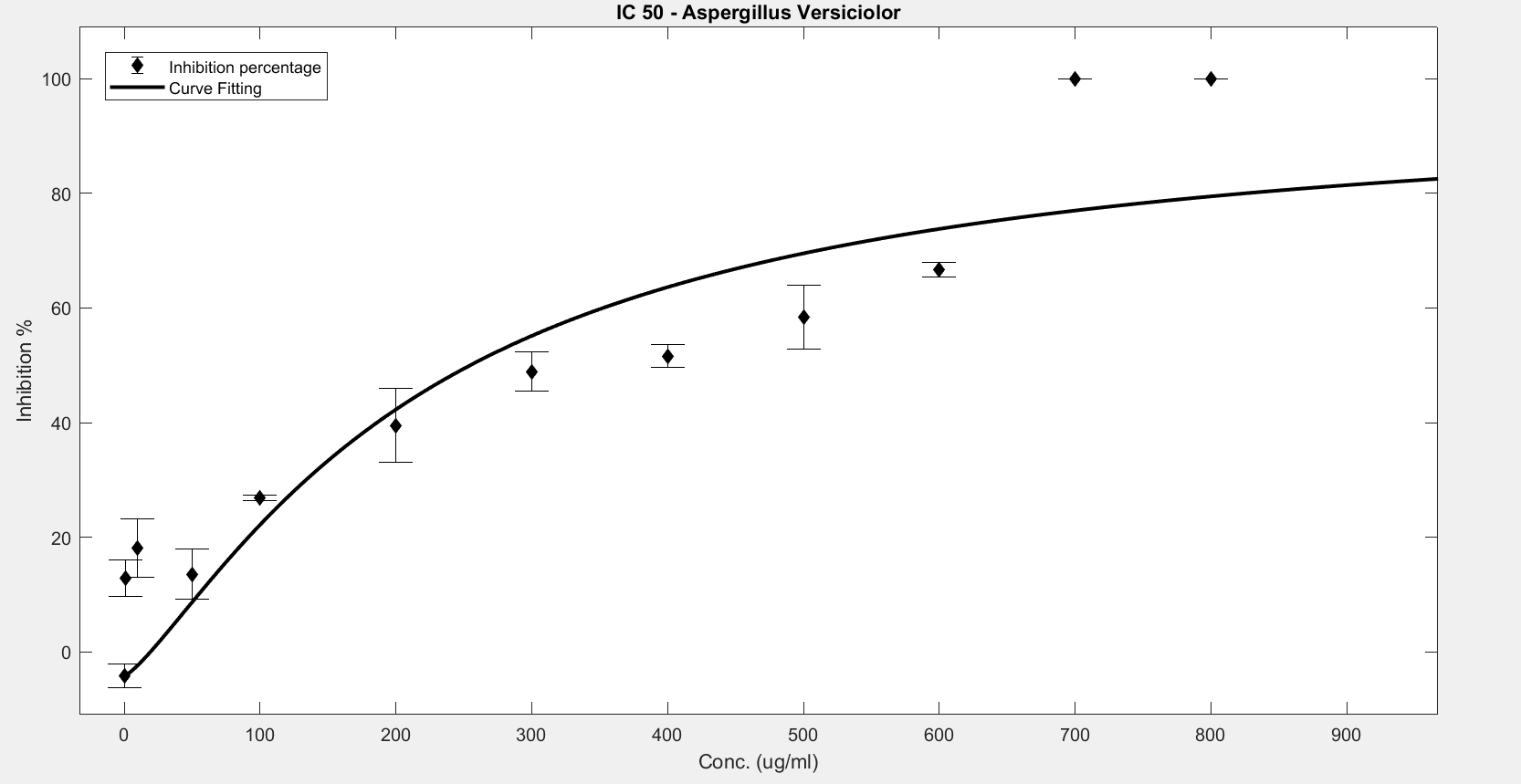
Figure 5. IC50 of Nipagin against A.versicolor using Method 1
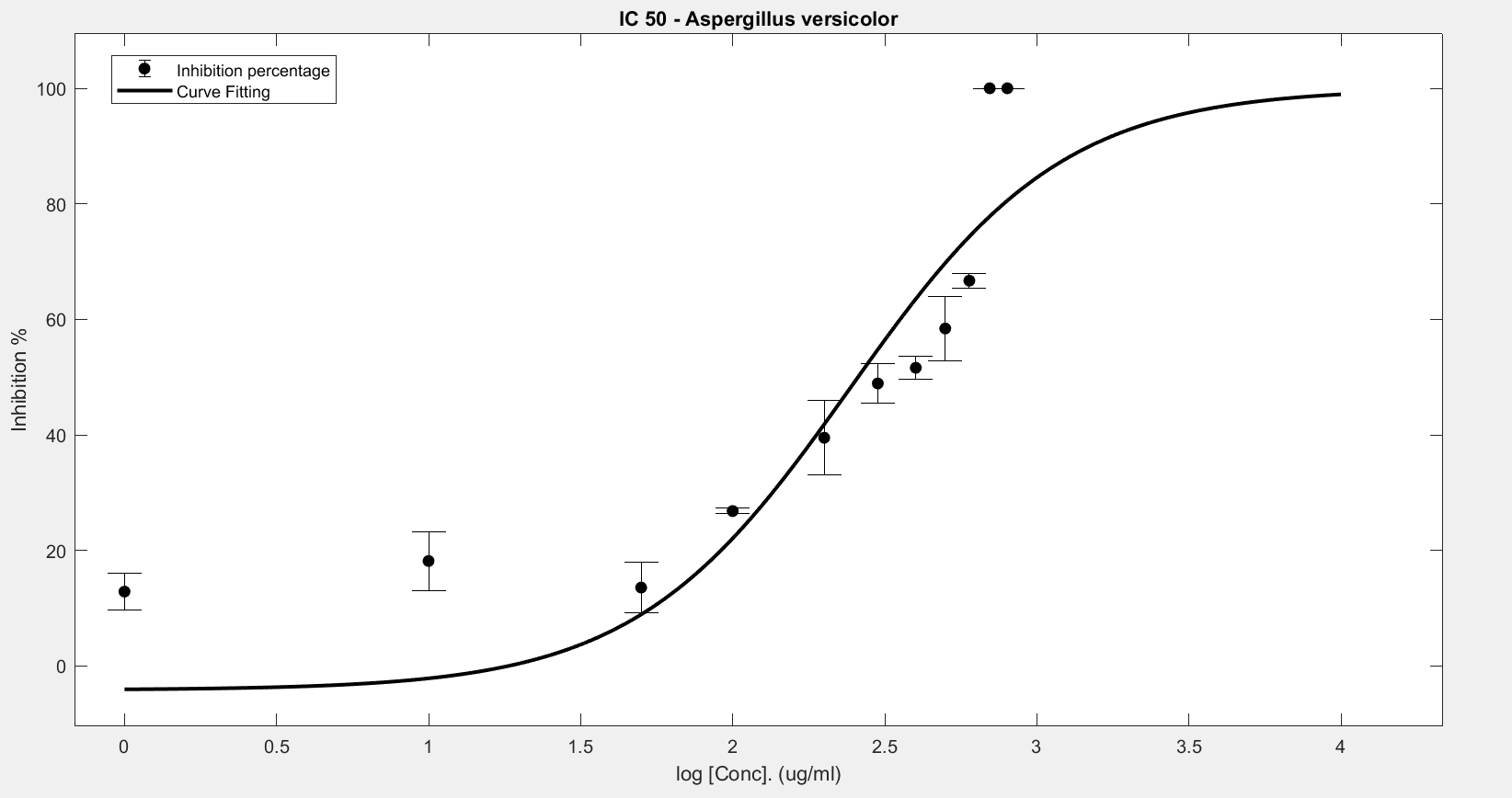
Figure 6. IC50 of Nipagin against A.versicolor using Method 2
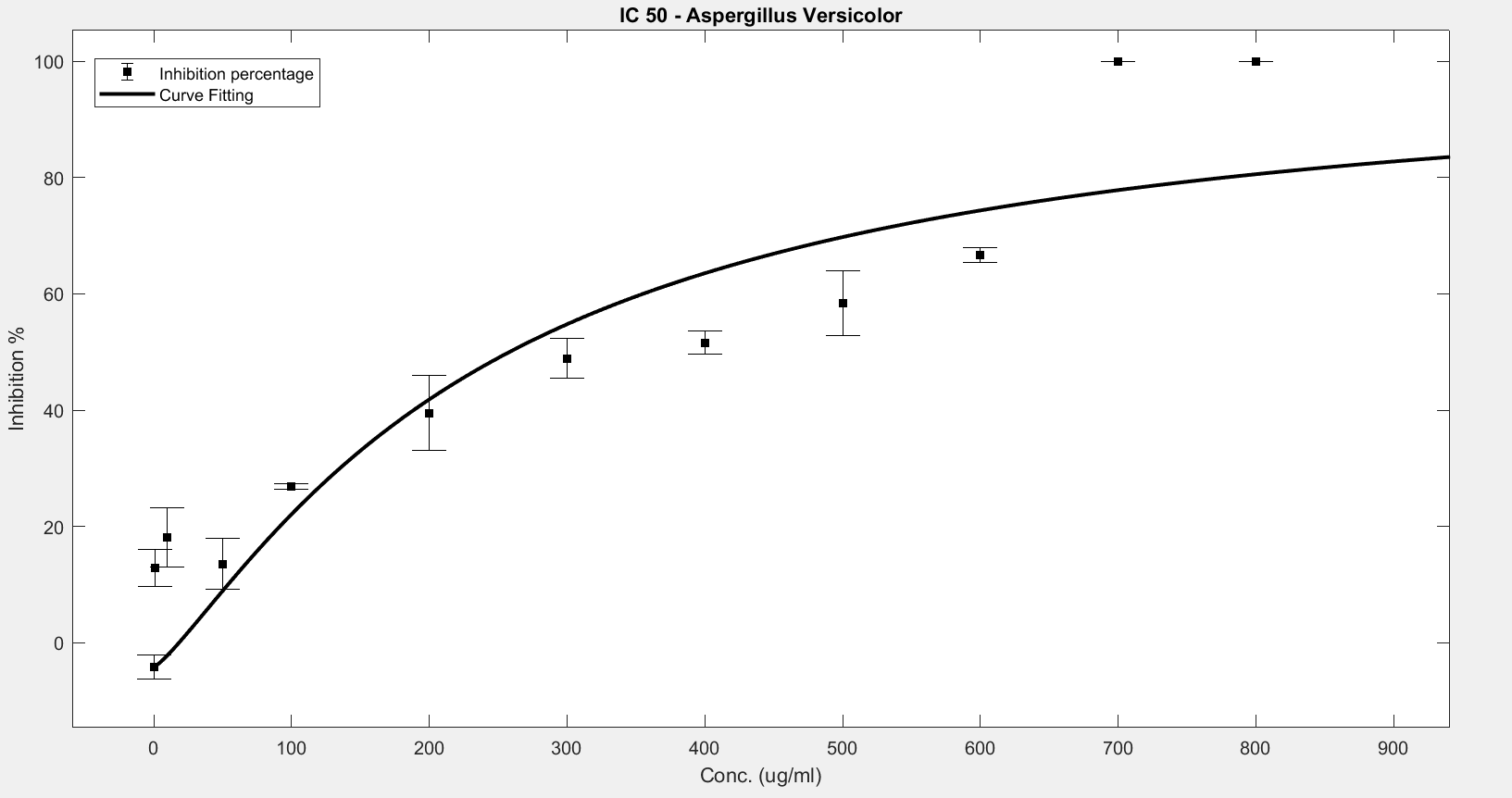
Figure 7. IC50 of Nipagin against A.versicolor using Method 3

Figure 8. IC50 of Nipagin against A.versicolor using Method 3
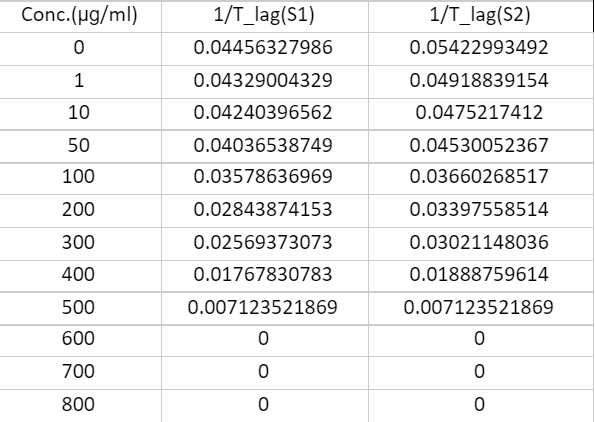
Figure 9. Data for Rhizopus Oryzae
Where
S1 = Sample 1
S2 = Sample 2
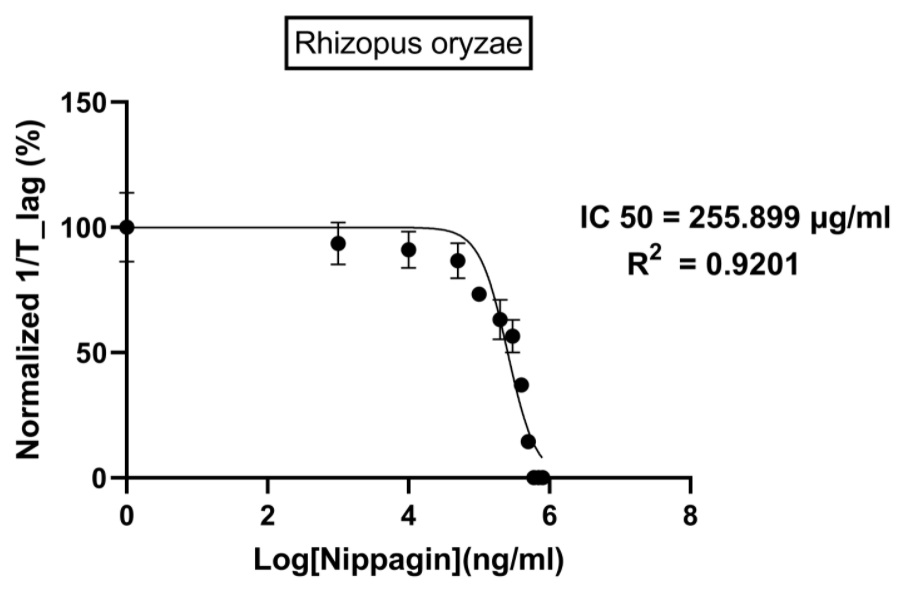
Figure 10.
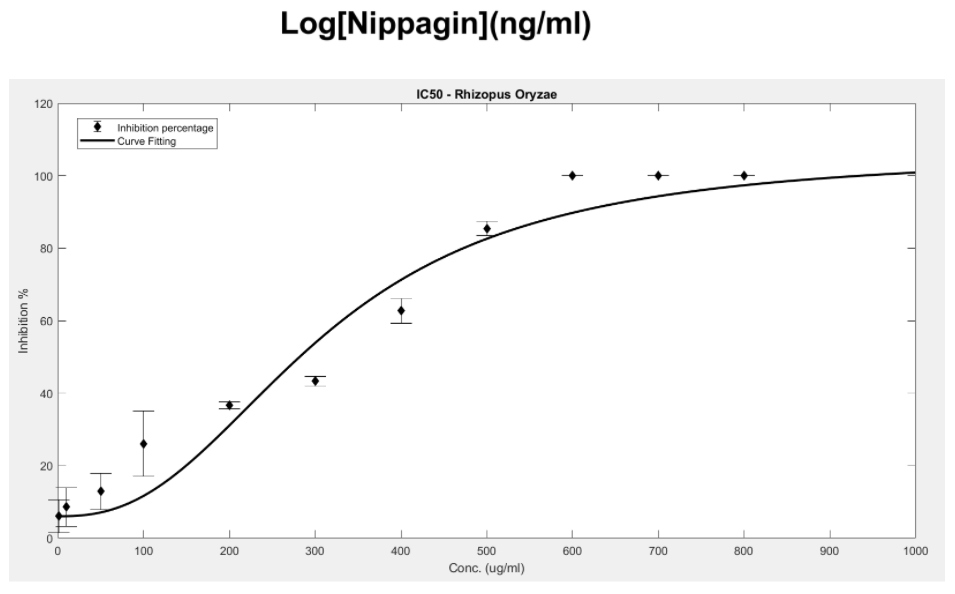
Figure 11. IC50 of Nipagin against R.oryzae using Method 1
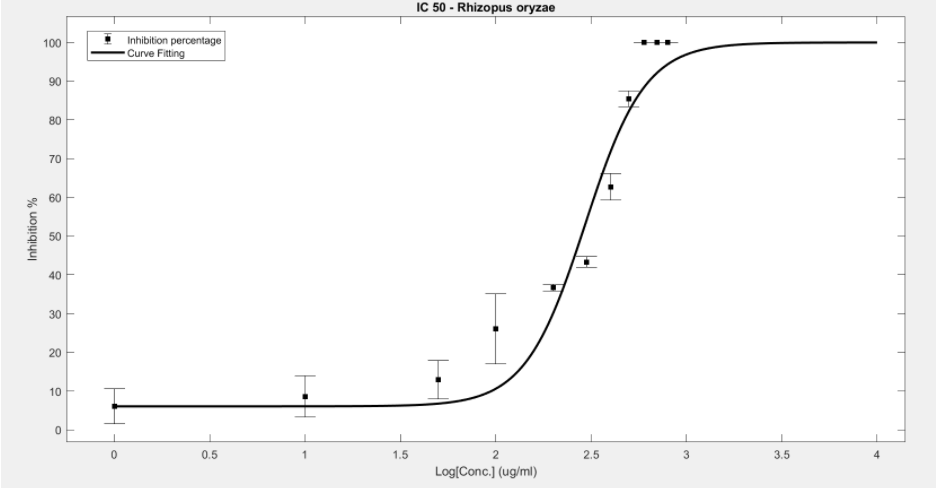
Figure 12. IC50 of Nipagin against R.oryzae using Method 2
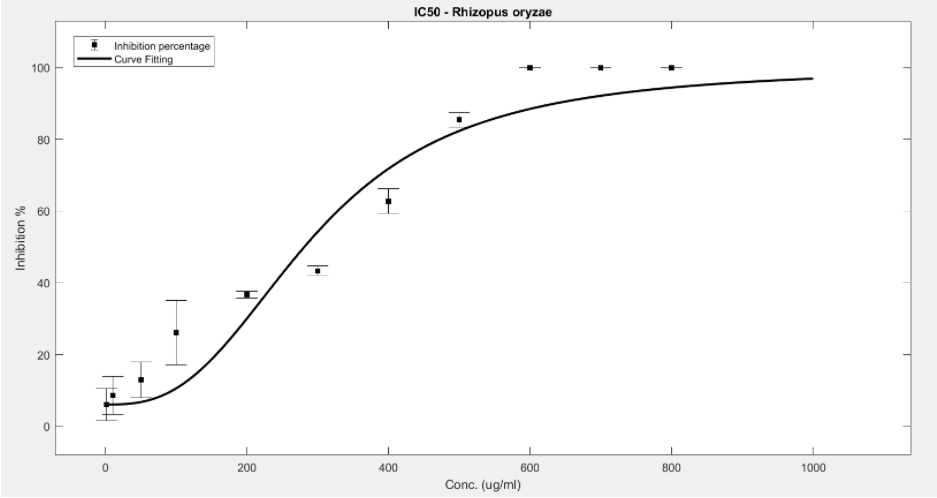
Figure 13. IC50 of Nipagin against R.oryzae using Method 3
Ligand receptor interaction
Protein estimation
The gene of our interest is expressed in the BL21 DE(3) strain of bacteria, whose expression will be under the inducible promoter. The inducer here is IPTG (Isopropyl β-d-1-thiogalactopyranoside).
For the genomic part of E. coli:
- Transcription of LacI mRNA
- Translation of LacI
- Formation of LacI and IPTG complex
- Passive diffusion of IPTG across the cell membrane of E.coli
$$\phi\xrightarrow{K_{tcI}}mRNA_{LacI}$$
Decay of LacI mRNA
$$mRNA_{LacI}\xrightarrow{K_{dmI}}\phi$$
\begin{equation}
\frac{d[mRNA_{LacI}]}{dt}=K_{tcI}-K_{dmI}[mRNA_{LacI}]
\end{equation}
$$mRNA_{LacI}\xrightarrow{K_{tl}}mRNA_{LacI}+LacI$$
Deacy of LacI
$$LacI\xrightarrow{K_{dpI}}\phi$$
\begin{equation}
\frac{d[LacI]}{dt}=K_{tl}[mRNA_{LacI}]-K_{dpI}[LacI]
\end{equation}
$$LacI+IPTG_{in}\xrightleftharpoons[K_{bI}]{K_{fI}}LacI-IPTG_{in}$$ \begin{equation} \frac{d[LacI-IPTG_{in}]}{dt}=K_{fI}[LacI][IPTG_{in}]-K_{bI}[LacI-IPTG_{in}] \end{equation}
$$IPTG_{ex}\xrightleftharpoons[K_{pdiff}]{K_{pdiff}}IPTG_{in}$$ \begin{equation} \frac{d[IPTG_{in}]}{dt}=K_{pdiff}([IPTG_{in}-[IPTG_{ex}])+K_{fdiff}([LacY\_ IPTG_{ex}]) \end{equation}